单位圆：三角学中的基本工具单位圆被定义为半径为1的圆，是理解与角度和长度相关的三角学概念的重要工具。

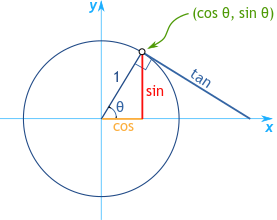单位圆位于图表的x轴和y轴交点处，为根据角度测量来评估正弦、余弦和正切值提供了清晰的参考框架。当角度θ为0°时，相应的三角函数值非常简单：0°的余弦为1，正弦为0，而正切（正弦与余弦的比值）也为0。

相反，当θ达到90°时，余弦降为0，而正弦达到1，使得正切因零除而未定义。深入探讨单位圆会发现正弦、余弦和正切的正负值之间的相互作用，这是由笛卡尔坐标决定的。

这种动态允许多种角度测量，鼓励用户与单位圆进行互动实验，以观察这些值的变化。

单位圆的核心是毕达哥拉斯定理，该定理表明在直角三角形中，斜边的平方等于其他两边的平方之和。

对于单位圆，这一定理简化为方程x² + y² = 1，其中x表示余弦，y表示正弦。这一关系最终形成一个有价值的三角恒等式：(cos(θ))² + (sin(θ))² = 1。

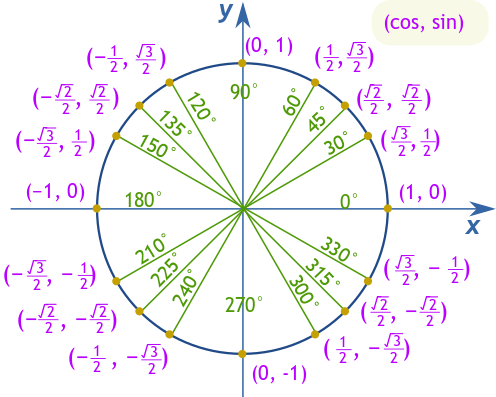
为了掌握30°、45°和60°等关键角度，记住它们的正弦、余弦和正切值是有利的。例如，在30°时，余弦为√3/2，正弦为1/2，正切为√3/3。在45°时，正弦和余弦均为√2/2，正切为1。最后，在60°时，余弦为1/2，正弦为√3/2，正切则上升到√3。

一个帮助记忆这些值的助记法是将余弦与递减的数字（3、2、1）关联，而将正弦与递增的数字（1、2、3）关联。

这种技巧简化了学习过程并增强了记忆保留。关于正切的计算，正切是正弦与余弦的比值，用户可以轻松推导出每个角度的值。例如，tan(30°)计算为sin(30°)/cos(30°)，结果为√3/3。同样，tan(45°)和tan(60°)的值也可以轻松推导。

为了加强记忆，绘制与这些角度对应的三角形是有益的。例如，绘制一个边长为2的三角形并进行分割，可以应用毕达哥拉斯定理来找到边的长度，从而帮助理解正弦和余弦值。

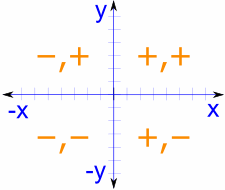
作为一个全面工具，单位圆涵盖了所有象限，并相应调整余弦和正弦值的符号。这种细致的理解对于确定第一象限之外的值至关重要。

总之，单位圆不仅提供了三角函数的视觉表示，而且作为三角学的基础概念，对于学生和从业人员来说至关重要。它的简单性掩盖了它在促进对数学原理更深入理解中的重要性，使其成为三角学研究的基石。