ইউনিট সার্কেল: ত্রিকোণমিতির একটি মৌলিক সরঞ্জাম ইউনিট সার্কেল, যা একক ব্যাসার্ধের একটি বৃত্ত হিসেবে সংজ্ঞায়িত, কোণ এবং দৈর্ঘ্য সম্পর্কিত ত্রিকোণমিতিক ধারণাগুলি বোঝার জন্য একটি অপরিহার্য সরঞ্জাম। 

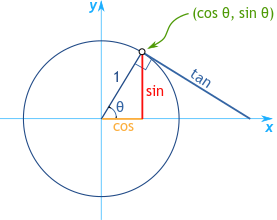একটি গ্রাফে x-axis এবং y-axis এর সংযোগস্থলে অবস্থিত, ইউনিট সার্কেল সাইন, কোসাইন এবং ট্যানজেন্ট মানগুলি কোণ পরিমাপের ভিত্তিতে মূল্যায়ন করার জন্য একটি পরিষ্কার রেফারেন্স ফ্রেম প্রদান করে। যখন কোণ θ কে 0° তে সেট করা হয়, তখন সংশ্লিষ্ট ত্রিকোণমিতিক মানগুলি সোজা হয়: 0° এর কোসাইন 1, সাইন 0, এবং ট্যানজেন্ট, সাইন এবং কোসাইনের অনুপাত হিসেবে, 0। 

অন্যদিকে, যখন θ 90° তে পৌঁছে, কোসাইন 0 তে নেমে আসে এবং সাইন 1 এ পৌঁছে যায়, ফলে ট্যানজেন্ট শূন্য দ্বারা ভাগের কারণে অজ্ঞাত হয়ে যায়। ইউনিট সার্কেলের গভীর অনুসন্ধান সাইন, কোসাইন, এবং ট্যানজেন্টের ধনাত্মক এবং ঋণাত্মক মানগুলির পারস্পরিক সম্পর্ককে প্রকাশ করে, যা কার্টেসিয়ান সমন্বয় দ্বারা নিয়ন্ত্রিত হয়। 

এই গতিশীলতা বিভিন্ন কোণ পরিমাপের জন্য অনুমতি দেয়, ব্যবহারকারীদের ইউনিট সার্কেলের সাথে ইন্টারেক্টিভভাবে পরীক্ষা করতে উত্সাহিত করে যাতে তারা এই মানগুলির পরিবর্তনগুলি পর্যবেক্ষণ করতে পারে। 

ইউনিট সার্কেলের কেন্দ্রে পিথাগোরীয় তত্ত্ব আছে, যা asserts যে একটি সোজা ত্রিভুজে, হাইপোটেনিউজের বর্গ অন্য দুই পাশের বর্গের সমষ্টির সমান। 

ইউনিট সার্কেলের জন্য, এই তত্ত্বটি x² + y² = 1 সমীকরণে সরল হয়, যেখানে x কোসাইন এবং y সাইনকে উপস্থাপন করে। এই সম্পর্কটি একটি মূল্যবান ত্রিকোণমিতিক পরিচিতিতে culminates: (cos(θ))² + (sin(θ))² = 1. 

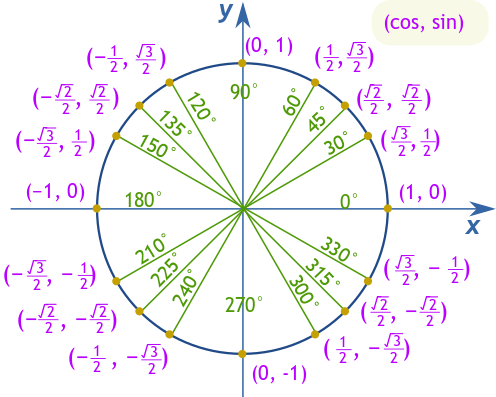
30°, 45°, এবং 60° এর মতো মূল কোণগুলি নেভিগেট করার জন্য, তাদের সাইন, কোসাইন, এবং ট্যানজেন্ট মানগুলি মনে রাখা সুবিধাজনক। উদাহরণস্বরূপ, 30° এ, কোসাইন √3/2, সাইন 1/2, এবং ট্যানজেন্ট √3/3। 45° এ, সাইন এবং কোসাইন উভয়ই √2/2, যা ট্যানজেন্টকে 1 দেয়। অবশেষে, 60° এ, কোসাইন 1/2, সাইন √3/2, এবং ট্যানজেন্ট √3 এ বৃদ্ধি পায়। 

এই মানগুলি মনে রাখতে সহায়তা করার জন্য একটি স্মরণীয় কৌশল হলো কোসাইনকে অবতরণকারী সংখ্যা (3, 2, 1) এবং সাইনকে উত্থানকারী সংখ্যা (1, 2, 3) এর সাথে সংযুক্ত করা। 

এই কৌশলটি শেখার প্রক্রিয়াকে সহজ করে এবং স্মৃতি ধরে রাখার ক্ষমতা বৃদ্ধি করে। ট্যানজেন্টের বিষয়ে, যা সাইন এবং কোসাইনের অনুপাত হিসেবে গণনা করা হয়, ব্যবহারকারীরা সহজেই প্রতিটি কোণের জন্য মানগুলি প্রাপ্ত করতে পারেন। উদাহরণস্বরূপ, tan(30°) গণনা করা হয় sin(30°)/cos(30°) হিসেবে, যা √3/3 দেয়। একইভাবে, tan(45°) এবং tan(60°) এর মানগুলি সহজেই নির্ধারণ করা যেতে পারে। 

মনে রাখার জন্য, এই কোণের সাথে সম্পর্কিত ত্রিভুজগুলি আঁকা উপকারী হতে পারে। উদাহরণস্বরূপ, 2 দৈর্ঘ্যের একটি ত্রিভুজ আঁকা এবং সেটিকে ভাগ করা হলে পিথাগোরীয় তত্ত্বের প্রয়োগের মাধ্যমে পাশগুলির দৈর্ঘ্য খুঁজে বের করা সম্ভব, যা সাইন এবং কোসাইন মানগুলি বোঝার জন্য সহায়ক। 

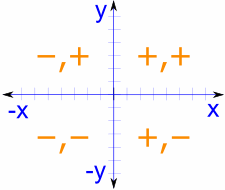
একটি ব্যাপক সরঞ্জাম হিসেবে, ইউনিট সার্কেল সকল কোয়ার্টারকে অন্তর্ভুক্ত করে, কোসাইন এবং সাইন মানগুলির চিহ্নগুলি যথাক্রমে সঠিকভাবে সমন্বয় করে। এই সূক্ষ্ম বোঝাপড়া প্রথম কোয়ার্টারের বাইরে মান নির্ধারণের জন্য অত্যন্ত গুরুত্বপূর্ণ। 

সারসংক্ষেপে, ইউনিট সার্কেল ত্রিকোণমিতিক ফাংশনের একটি ভিজ্যুয়াল উপস্থাপনাই নয়, বরং ত্রিকোণমিতির একটি মৌলিক ধারণা, যা ছাত্র এবং পেশাদারদের জন্য অপরিহার্য। এর সরলতা গণিতের মৌলিক নীতিগুলির গভীর ধারণাকে সহজতর করতে সাহায্য করে, যা এটিকে ত্রিকোণমিতির অধ্যয়নের একটি আদর্শ ভিত্তি তৈরি করে।