યુનિટ સર્કલ: ત્રિકોણમિતીની એક મૂળભૂત સાધન યુનિટ સર્કલ, જેને એકની વ્યાસવાળા સર્કલ તરીકે વ્યાખ્યાયિત કરવામાં આવે છે, તે ખૂણાંઓ અને લંબાઈઓ સાથે સંબંધિત ત્રિકોણમિતી સંકલ્પનાઓને સમજવા માટે એક મહત્વપૂર્ણ સાધન છે. 

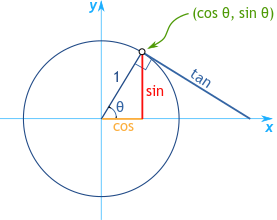ગ્રાફમાં x-અક્ષ અને y-અક્ષના સંકોચન પર સ્થિત, યુનિટ સર્કલ ખૂણાના માપને આધારે સાઇન, કોશીન અને ટેંજન્ટ મૂલ્યોને આંકલન કરવા માટે એક સ્પષ્ટ સંદર્ભ ફ્રેમ પ્રદાન કરે છે. જ્યારે ખૂણો, જેને θ તરીકે દર્શાવવામાં આવે છે, 0° પર સેટ કરવામાં આવે છે, ત્યારે સંબંધિત ત્રિકોણમિતી મૂલ્યો સરળ છે: 0° ના કોશીન 1 છે, સાઇન 0 છે, અને ટેંજન્ટ, જે સાઇન અને કોશીનનો અનુપાત છે, તે પણ 0 છે. 

વિપરીત રીતે, જ્યારે θ 90° પહોંચે છે, ત્યારે કોશીન 0 પર નીચે આવે છે જયારે સાઇન 1 પર હળવાશ પામે છે, જેથી ટેંજન્ટ અસ્પષ્ટ બની જાય છે કારણ કે શૂન્ય દ્વારા વિભાજન થાય છે. યુનિટ સર્કલની વધુ ઊંડાણમાં તપાસ કરવાથી સાઇન, કોશીન અને ટેંજન્ટના નવા અને નકારાત્મક મૂલ્યો વચ્ચેના આંતરસંબંધને દર્શાવે છે, જે કાર્ટેશિયન સંકલ્પનાઓ દ્વારા નિયંત્રિત થાય છે. 

આ ગતિશીલતા વિવિધ પ્રકારના ખૂણાના માપો માટેની પરવાનગી આપે છે, યૂઝર્સને યુનિટ સર્કલ સાથે ઇન્ટરેક્ટિવ રીતે પ્રયોગ કરવા માટે પ્રોત્સાહિત કરે છે જેથી તેઓ આ મૂલ્યોમાંના પરિવર્તનોને અવલોકન કરી શકે. 

યુનિટ સર્કલના દિલમાં પાયથાગોરસ થિયોરમ છે, જે કહે છે કે સીધા ત્રિકોણમાં, હાઇપોથેન્યુઝનું વર્ગ અન્ય બે બાજુઓના વર્ગોના સરવાળા સમાન છે. 

યુનિટ સર્કલ માટે, આ થિયોરમ x² + y² = 1ના સમીકરણમાં સરળ બનાવે છે, જ્યાં x કોશીનનું પ્રતિનિધિત્વ કરે છે અને y સાઇનનું પ્રતિનિધિત્વ કરે છે. આ સંબંધ એક મૂલ્યવાન ત્રિકોણમિતી ઓળખાણમાં સમાપ્તિ કરે છે: (cos(θ))² + (sin(θ))² = 1. 

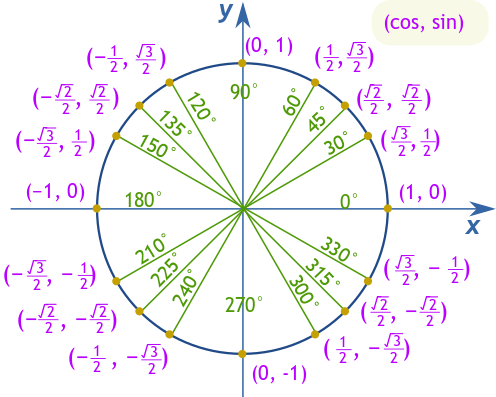
30°, 45°, અને 60° જેવા મુખ્ય ખૂણાઓને અનુક્રમણ કરવામાં, તેમના સાઇન, કોશીન અને ટેંજન્ટ મૂલ્યો યાદ રાખવાં ફાયદાકારક છે. ઉદાહરણ તરીકે, 30° પર, કોશીન √3/2 છે, સાઇન 1/2 છે, અને ટેંજન્ટ √3/3 છે. 45° પર, સાઇન અને કોશીન બંને √2/2 છે, જે 1 ના ટેંજન્ટ આપે છે. છેલ્લે, 60° પર, કોશીન 1/2 છે, સાઇન √3/2 છે, અને ટેંજન્ટ √3 સુધી વધે છે. 

આ મૂલ્યોને યાદ રાખવામાં મદદ માટે એક મnemોનિકમાં કોશીનને ઉતરતા નંબરો (3, 2, 1) અને સાઇનને ઊંચા નંબરો (1, 2, 3) સાથે જોડવું શામેલ છે. 

આ પદ્ધતિ શીખવા માટે સરળ બનાવે છે અને સ્મૃતિ જાળવવામાં સુધારે છે. ટેંજન્ટના મામલે, જે સાઇન અને કોશીનના અનુપાત તરીકે ગણવામાં આવે છે, વપરાશકર્તાઓ દરેક ખૂણાના માટે મૂલ્યો સરળતાથી શોધી શકે છે. ઉદાહરણ તરીકે, tan(30°) ગણવામાં આવે છે sin(30°)/cos(30°), જે √3/3 આપે છે. સમાન રીતે, tan(45°) અને tan(60°) ના મૂલ્યો સરળતાથી નીકળે છે. 

સ્મૃતિને મજબૂત બનાવવા માટે, આ ખૂણાઓના અનુરૂપ ત્રિકોણો ખીંચવું ફાયદાકારક હોઈ શકે છે. ઉદાહરણ તરીકે, 2 ની બાજુઓના લંબાઈ ધરાવતી ત્રિકોણને ખીંચવાથી પાયથાગોરસ થિયોરમનો ઉપયોગ કરીને બાજુઓના લંબાઈઓ શોધવા માટે મદદ મળી શકે છે, જે અંતે સાઇન અને કોશીનના મૂલ્યોની સમજૂતીમાં સહાય કરે છે. 

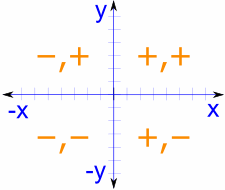
એક વ્યાપક સાધન તરીકે, યુનિટ સર્કલ તમામ ક્વાડ્રન્ટ્સને આવરી લે છે, જે મુજબ કોશીન અને સાઇનના મૂલ્યોના ચિહ્નોને સમાયોજિત કરે છે. આ જટિલ સમજણ પ્રથમ ક્વાડ્રન્ટથી વધુ મૂલ્યો નક્કી કરવા માટે મહત્વપૂર્ણ છે. 

અંતમાં, યુનિટ સર્કલ માત્ર ત્રિકોણમિતી ફંક્શનનો દૃષ્ટિ પ્રતિનિધિત્વ નથી આપીતી, પરંતુ તે ત્રિકોણમિતીમાં એક આધારભૂત સંકલ્પના તરીકે પણ કાર્ય કરે છે, જે વિદ્યાર્થીઓ અને વ્યાવસાયિકોને માટે મહત્વપૂર્ણ છે. તેની સરળતા ગણિતના સિદ્ધાંતોને વધુ ઊંડાઈથી સમજવા માટે સહાય કરે છે, જે તેને ત્રિકોણમિતી અભ્યાસનો એક ખૂણાકાર બનાવે છે.