الدائرة الوحدة: أداة أساسية في علم المثلثات تُعرف الدائرة الوحدة بأنها دائرة نصف قطرها واحد، وتعتبر أداة أساسية لفهم المفاهيم المثلثية المتعلقة بالزوايا والأطوال. 

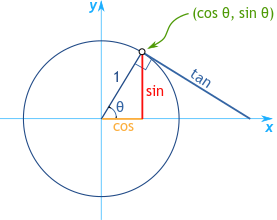تقع الدائرة الوحدة عند تقاطع المحور السيني والمحور الصادي على الرسم البياني، مما يوفر إطاراً مرجعياً واضحاً لتقييم قيم الجيب، وجيب التمام، والظل بناءً على قياسات الزاوية. عندما تكون الزاوية، الممثلة بـ θ، تساوي 0°، تكون القيم المثلثية المقابلة بسيطة: جيب التمام لـ 0° هو 1، والجيب هو 0، والظل، كونه نسبة الجيب إلى جيب التمام، هو أيضاً 0. 

على النقيض، عندما تصل θ إلى 90°، ينخفض جيب التمام إلى 0 بينما يصل الجيب إلى 1، مما يجعل الظل غير معرف بسبب القسمة على صفر. يكشف استكشاف أعمق للدائرة الوحدة عن التفاعل بين القيم الموجبة والسالبة للجيب، وجيب التمام، والظل، وفقاً للإحداثيات الكارتيزية. 

تتيح هذه الديناميكية مجموعة واسعة من قياسات الزوايا، مما يحفز المستخدمين على التجربة التفاعلية مع الدائرة الوحدة لمراقبة هذه التحولات في القيم. 

في قلب الدائرة الوحدة تكمن نظرية فيثاغورس، التي تؤكد أنه في مثلث قائم الزاوية، يساوي مربع الوتر مجموع مربعات الضلعين الآخرين. 

بالنسبة للدائرة الوحدة، تُبسط هذه النظرية إلى المعادلة x² + y² = 1، حيث تمثل x جيب التمام وy تمثل الجيب. تؤدي هذه العلاقة إلى هوية مثلثية قيمة: (cos(θ))² + (sin(θ))² = 1. 

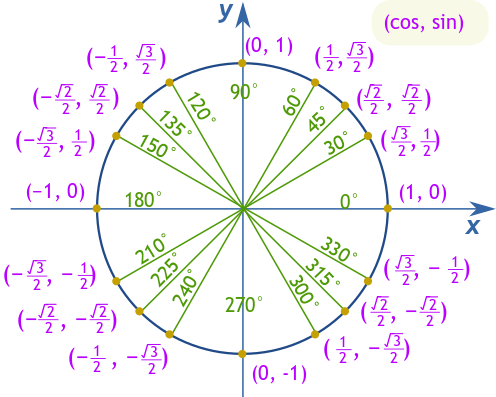
لتسهيل التعامل مع الزوايا الرئيسية مثل 30°، 45°، و60°، يُعتبر حفظ قيم الجيب، وجيب التمام، والظل مفيداً. على سبيل المثال، عند 30°، يكون جيب التمام √3/2، والجيب 1/2، والظل √3/3. عند 45°، يساوي كل من الجيب وجيب التمام √2/2، مما ينتج عنه ظل يساوي 1. وأخيراً، عند 60°، يكون جيب التمام 1/2، والجيب √3/2، ويصل الظل إلى √3. 

تشمل تقنية تذكارية للمساعدة في تذكر هذه القيم ربط جيب التمام بالأرقام المتناقصة (3، 2، 1) والجيب بالأرقام المتزايدة (1، 2، 3). 

تبسط هذه التقنية عملية التعلم وتعزز الاحتفاظ بالمعلومات. فيما يتعلق بالظل، الذي يُحسب كنسبة الجيب إلى جيب التمام، يمكن للمستخدمين استنتاج القيم لكل زاوية بسهولة. على سبيل المثال، يتم حساب tan(30°) كالتالي: sin(30°)/cos(30°)، مما ينتج عنه √3/3. وبالمثل، يمكن استنتاج القيم لـ tan(45°) وtan(60°) بسهولة. 

لتعزيز الذاكرة، يمكن أن يكون رسم مثلثات تتوافق مع هذه الزوايا مفيداً. على سبيل المثال، رسم مثلث بأطوال أضلاع 2 وقسمه يسمح بتطبيق نظرية فيثاغورس لإيجاد أطوال الأضلاع، مما يساعد في فهم قيم الجيب وجيب التمام. 

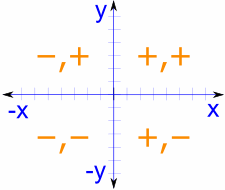
كأداة شاملة، تشمل الدائرة الوحدة جميع الأرباع، مما يضبط إشارات قيم جيب التمام والجيب وفقاً لذلك. هذه الفهم الدقيق أمر حاسم لتحديد القيم خارج الربع الأول. 

في الختام، لا تتيح الدائرة الوحدة فقط تمثيلاً بصرياً للدوال المثلثية ولكنها أيضاً تشكل مفهومًا أساسيًا في علم المثلثات، وهو ضروري للطلاب والممارسين على حد سواء. إن بساطتها تخفي أهميتها في تسهيل فهم أعمق للمبادئ الرياضية، مما يجعلها حجر الزاوية في دراسة المثلثات.