യൂണിറ്റ് സർക്കിൾ: ട്രിഗണോമെട്രിയിൽ ഒരു അടിസ്ഥാന ഉപകരണം ഒരു അളവ് ഒന്നാണെന്ന് നിർവചിക്കപ്പെട്ട യൂണിറ്റ് സർക്കിൾ, കോണുകളും ദൈർഘ്യങ്ങളും സംബന്ധിച്ച ട്രിഗണോമെട്രിക് ആശയങ്ങളെ മനസ്സിലാക്കുന്നതിനുള്ള ഒരു പ്രധാന ഉപകരണമാണു. 

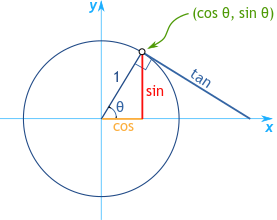ഗ്രാഫിൽ x-അക്ഷവും y-അക്ഷവും ചേരുന്ന സ്ഥലത്ത് സ്ഥിതിചെയ്യുന്ന യൂണിറ്റ് സർക്കിൾ, കോണുകളുടെ അളവുകൾ അടിസ്ഥാനമാക്കിയുള്ള സൈൻ, കോസൈൻ, ടാങ്കന്റ് മൂല്യങ്ങൾ വിലയിരുത്തുന്നതിനുള്ള ഒരു വ്യക്തമായ റഫറൻസ് ഫ്രെയിം നൽകുന്നു. θ എന്ന കോണിന്റെ അളവ് 0° ആയി നിശ്ചയിക്കുമ്പോൾ, അനുബന്ധ ട്രിഗണോമെട്രിക് മൂല്യങ്ങൾ വളരെ ലളിതമാണ്: 0° ന്റെ കോസൈൻ 1 ആണ്, സൈൻ 0 ആണ്, ടാങ്കന്റ്, സൈൻ-ന്റെ കോസൈനോട് ഉള്ള അനുപാതം ആയതിനാൽ, 0 ആകും. 

അതിന്റെ മറുവശത്തുക, θ 90° ആയി എത്തുമ്പോൾ, കോസൈൻ 0-ലേക്ക് താഴ്ന്നു, എന്നാൽ സൈൻ 1-ൽ ഉയരുന്നു, ടാങ്കന്റ് 0-ന്റെ ഭാഗം കൊണ്ടു നിർവാച്യം ചെയ്യാനാവാത്തതാകും. യൂണിറ്റ് സർക്കിൾയുടെ ആഴത്തിൽ നിന്നുള്ള ഒരു അന്വേഷണത്തിൽ, കാർട്ടേഷ്യൻ കോഓർഡിനേറ്റുകൾ പ്രകാരം സൈൻ, കോസൈൻ, ടാങ്കന്റ് ന്റെ പോസിറ്റീവ്, നെഗറ്റീവ് മൂല്യങ്ങൾ തമ്മിലുള്ള ബന്ധം വ്യക്തമാക്കുന്നു. 

ഈ ഗതി, കോണുകളുടെ അളവുകൾക്കായി വ്യാപകമായ മാറ്റങ്ങൾ അനുവദിക്കുന്നു, ഉപയോക്താക്കൾക്ക് മൂല്യങ്ങളിൽ നടക്കുന്ന ഈ മാറ്റങ്ങൾ നിരീക്ഷിക്കാൻ യൂണിറ്റ് സർക്കിൾക്കൊപ്പം ഇന്ററാക്ടീവ് ആയി പരീക്ഷിക്കാൻ പ്രേരിപ്പിക്കുന്നു. 

യൂണിറ്റ് സർക്കിൾയുടെ ഹൃദയത്തിൽ പൈതഗോറസ് തിയറിയാണ്, അത് ഒരു വലുത് ത്രികോണത്തിൽ, ഹൈപൊട്ടന്യുസിന്റെ ചതുരം മറ്റ് രണ്ട് കഷണങ്ങളുടെ ചതുരങ്ങളുടെ മൊത്തത്തിന് തുല്യമാണ് എന്ന് ഉറപ്പിക്കുന്നു. 

യൂണിറ്റ് സർക്കിളിൽ, ഈ തിയറി x² + y² = 1 എന്ന സമവാക്യത്തിലേക്ക് ലഘുവാക്കുന്നു, ഇവിടെ x കോസൈനും y സൈനുമാണ്. ഈ ബന്ധം ഒരു വിലപ്പെട്ട ട്രിഗണോമെട്രിക് ഐഡന്റിറ്റിയിലേക്ക് എത്തുന്നു: (cos(θ))² + (sin(θ))² = 1. 

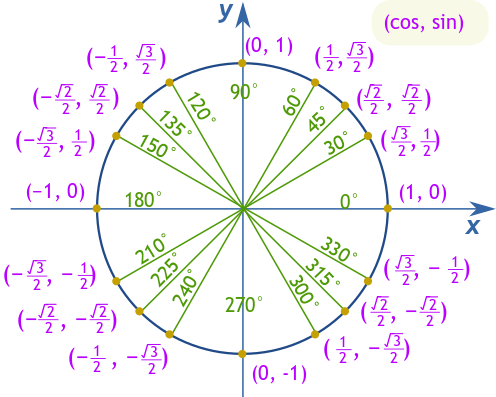
30°, 45°, 60° പോലെയുള്ള പ്രധാന കോണുകൾ മനസ്സിലാക്കാൻ, അവരുടെ സൈൻ, കോസൈൻ, ടാങ്ക് മൂല്യങ്ങൾ ഓർമ്മിക്കുക അനുകൂലമാണ്. ഉദാഹരണത്തിന്, 30° ൽ, കോസൈൻ √3/2, സൈൻ 1/2, ടാങ്ക് √3/3 ആണ്. 45° ൽ, സൈൻയും കോസൈനും √2/2 ആകുന്നു, 1 ന്റെ ടാങ്ക് നൽകുന്നു. അവസാനം, 60° ൽ, കോസൈൻ 1/2, സൈൻ √3/2, ടാങ്ക് √3 ആയി ഉയരുന്നു. 

ഈ മൂല്യങ്ങൾ ഓർമിക്കാൻ സഹായിക്കുന്ന ഒരു മ്നemonic കോസൈനെ കുറിച്ചുള്ള സംഖ്യകൾ (3, 2, 1) ഒപ്പം സൈനുമായി ഉയര്‍ന്ന സംഖ്യകൾ (1, 2, 3) ബന്ധിപ്പിക്കുന്നത് ഉൾക്കൊള്ളുന്നു. 

ഈ സാങ്കേതികം പഠനം ലളിതമാക്കുകയും ഓർമ്മശക്തി വർദ്ധിപ്പിക്കുകയും ചെയ്യുന്നു. ടാങ്ക്, സൈൻ-ന്റെ കോസൈനോട് ഉള്ള അനുപാതമായി കണക്കാക്കുമ്പോൾ, ഉപയോക്താക്കൾക്ക് ഓരോ കോണിനും മൂല്യങ്ങൾ എളുപ്പത്തിൽ വരുത്താൻ കഴിയും. ഉദാഹരണത്തിന്, tan(30°) സൈൻ(30°)/കോസൈൻ(30°) എന്നതുപോലെ കണക്കാക്കി √3/3 ആയി ആണ്. tan(45°)യും tan(60°) ന്റെയും മൂല്യങ്ങൾ എളുപ്പത്തിൽ കണ്ടെത്താൻ കഴിയും. 

ഓർമ്മയെ ശക്തിപ്പെടുത്തുന്നതിനായി, ഈ കോണുകൾക്ക് അനുയോജ്യമായ ത്രികോണങ്ങൾ വരയ്ക്കുന്നത് പ്രയോജനകരമായിരിക്കും. ഉദാഹരണത്തിന്, 2 എന്ന ദൈർഘ്യങ്ങളുള്ള ഒരു ത്രികോണം വരയ്ക്കുന്നത്, പിൻഗാമി തിയറിയുടെ ഉപയോഗം കൊണ്ട് കഷണങ്ങളുടെ ദൈർഘ്യങ്ങൾ കണ്ടെത്തുന്നതിനും, സൈൻ, കോസൈൻ മൂല്യങ്ങൾ മനസ്സിലാക്കുന്നതിനും സഹായിക്കുന്നു. 

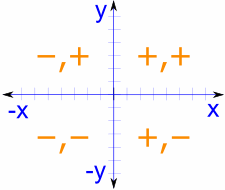
ഒരു സമഗ്ര ഉപകരണമെന്ന നിലയിൽ, യൂണിറ്റ് സർക്കിൾ എല്ലാ ക്വാഡ്രന്റുകളെയും ഉൾക്കൊള്ളുന്നു, കോസൈൻ, സൈൻ മൂല്യങ്ങളുടെ അടിസ്ഥാനം മാറ്റുന്നു. ഈ സൂക്ഷ്മമായ മനസ്സിലാക്കൽ, ആദ്യ ക്വാഡ്രന്റിന് പുറമെ മൂല്യങ്ങൾ കണ്ടെത്തുന്നതിന് നിർണായകമാണ്. 

അവസാനം, യൂണിറ്റ് സർക്കിൾ ട്രിഗണോമെട്രിക് ഫംഗ്ഷനുകളുടെ ദൃശ്യ പ്രതിനിധാനം മാത്രമല്ല; ഇത് വിദ്യാർത്ഥികൾക്കും പ്രായോഗികരായവർക്കുമായി അടിസ്ഥാനപരമായ ഒരു ആശയം കൂടിയാണ്. അതിന്റെ ലളിതത്വം അതിന്റെ പ്രാധാന്യത്തെ മറയ്ക്കുന്നു, ഗണിതാത്മക സിദ്ധാന്തങ്ങളുടെ ആഴത്തിൽ മനസ്സിലാക്കാൻ സഹായിക്കുന്നതിൽ, ഇത് ട്രിഗണോമെട്രിക് പഠനത്തിന്റെ അടിത്തറയാണ്.