یونٹ سرکل: مثلثیات میں ایک بنیادی ذریعہ یونٹ سرکل، جو ایک ایسے دائرے کے طور پر بیان کیا جاتا ہے جس کا رداس ایک ہے، زاویوں اور لمبائیوں سے متعلق مثلثاتی تصورات کو سمجھنے کے لیے ایک اہم ذریعہ ہے۔ 

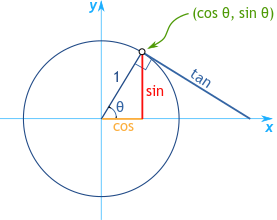یہ گراف پر x-axis اور y-axis کی تقاطع پر واقع ہے، یونٹ سرکل سائن، کوسائن، اور ٹینجنٹ کی قیمتوں کا اندازہ کرنے کے لیے ایک واضح حوالہ فریم فراہم کرتا ہے۔ جب زاویہ، جسے θ سے ظاہر کیا جاتا ہے، 0° پر رکھا جاتا ہے تو اس کے مطابق مثلثاتی قیمتیں آسان ہوتی ہیں: 0° کا کوسائن 1 ہے، سائن 0 ہے، اور ٹینجنٹ، جو سائن اور کوسائن کا تناسب ہے، بھی 0 ہے۔ 

اس کے برعکس، جب θ 90° تک پہنچتا ہے تو کوسائن 0 پر آ جاتا ہے جبکہ سائن 1 پر پہنچ جاتا ہے، جس کی وجہ سے ٹینجنٹ کی تعریف ختم ہو جاتی ہے کیونکہ یہ صفر سے تقسیم ہو رہا ہے۔ یونٹ سرکل کی مزید گہرائی میں جا کر سائن، کوسائن، اور ٹینجنٹ کی مثبت اور منفی قیمتوں کے درمیان تعلق کا انکشاف ہوتا ہے، جو کارٹیسین کوآرڈینیٹس کے ذریعے طے ہوتا ہے۔ 

یہ متحرک حالت مختلف زاویوں کی پیمائش کی اجازت دیتی ہے، جو صارفین کو یونٹ سرکل کے ساتھ تجرباتی طور پر قیمتوں کی تبدیلیوں کا مشاہدہ کرنے کی ترغیب دیتی ہے۔ 

یونٹ سرکل کے مرکز میں فیثاغورث کا نظریہ ہے، جو یہ بتاتا ہے کہ کسی مستطیل مثلث میں، ہائپوٹینوس کا مربع دوسرے دو اطراف کے مربعوں کے مجموعے کے برابر ہوتا ہے۔ 

یونٹ سرکل کے لیے، یہ نظریہ سادہ ہو کر درج ذیل مساوات میں تبدیل ہو جاتا ہے x² + y² = 1، جہاں x کوسائن کی نمائندگی کرتا ہے اور y سائن کی۔ یہ تعلق ایک قیمتی مثلثاتی شناخت میں culminates: (cos(θ))² + (sin(θ))² = 1. 

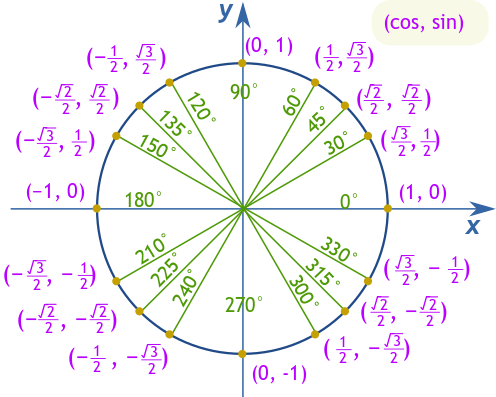
کلیدی زاویوں جیسے 30°, 45°, اور 60° کو نیویگیٹ کرنے کے لیے، ان کی سائن، کوسائن، اور ٹینجنٹ کی قیمتوں کو یاد رکھنا فائدہ مند ہے۔ مثال کے طور پر، 30° پر، کوسائن √3/2، سائن 1/2، اور ٹینجنٹ √3/3 ہے۔ 45° پر، دونوں سائن اور کوسائن √2/2 کے برابر ہیں، جو ایک کے ٹینجنٹ کو پیدا کرتا ہے۔ آخر میں، 60° پر، کوسائن 1/2، سائن √3/2، اور ٹینجنٹ √3 تک بڑھتا ہے۔ 

ان قیمتوں کو یاد رکھنے کے لیے ایک میمونی کوسائن کو نیچے کی جانب بڑھتے ہوئے نمبروں (3، 2، 1) اور سائن کو اوپر کی جانب بڑھتے ہوئے نمبروں (1، 2، 3) سے منسلک کرنا شامل ہے۔ 

یہ تکنیک سیکھنے کو سادہ بناتی ہے اور یادداشت کو بہتر کرتی ہے۔ ٹینجنٹ کی بات کریں تو، جو سائن اور کوسائن کے تناسب کے طور پر حساب کیا جاتا ہے، صارفین ہر زاویے کے لیے قیمتیں آسانی سے حاصل کر سکتے ہیں۔ مثال کے طور پر، tan(30°) کو sin(30°)/cos(30°) کے طور پر حساب کیا جاتا ہے، جو √3/3 بنتا ہے۔ اسی طرح، tan(45°) اور tan(60°) کی قیمتیں بھی آسانی سے نکالی جا سکتی ہیں۔ 

یادداشت کو مستحکم کرنے کے لیے، ان زاویوں کے مطابق مثلثیں بنانا فائدہ مند ثابت ہو سکتا ہے۔ مثال کے طور پر، 2 کی جانب سے طول و عرض والے مثلث کو بنانا اور تقسیم کرنا فیثاغورث کے نظریے کا استعمال کرنے کی اجازت دیتا ہے تاکہ اطراف کی لمبائیوں کو معلوم کیا جا سکے، آخرکار سائن اور کوسائن کی قیمتوں کی سمجھ بوجھ میں مدد ملتی ہے۔ 

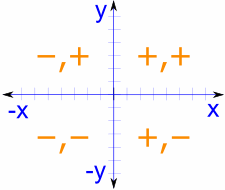
ایک جامع ذریعہ کے طور پر، یونٹ سرکل تمام چوتھائیوں کا احاطہ کرتا ہے، کوسائن اور سائن کی قیمتوں کے نشانات کو مناسب طریقے سے ایڈجسٹ کرتا ہے۔ یہ باریک بینی سے سمجھنا پہلی چوتھائی سے آگے کی قیمتوں کا تعین کرنے کے لیے اہم ہے۔ 

خلاصے کے طور پر، یونٹ سرکل نہ صرف مثلثاتی افعال کی بصری نمائندگی پیش کرتا ہے بلکہ یہ مثلثیات میں ایک بنیادی تصور کے طور پر بھی کام کرتا ہے، جو طلباء اور پیشہ ور افراد دونوں کے لیے ضروری ہے۔ اس کی سادگی اس کی اہمیت کو چھپاتی ہے، جو ریاضی کے اصولوں کی گہرائی کو سمجھنے میں مدد دیتی ہے، جسے مثلثاتی مطالعے کی بنیاد سمجھا جاتا ہے۔