युनिट सर्कल: त्रिकोणमितीत एक मूलभूत साधन युनिट सर्कल, जो एकाच्या त्रिज्येसह परिभाषित केलेला एक वर्तुळ आहे, हा कोन आणि लांबीशी संबंधित त्रिकोणमितीय संकल्पनांचा समजून घेण्यासाठी एक आवश्यक साधन म्हणून कार्य करते. 

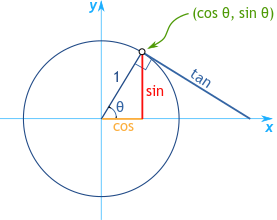ग्राफवर x-अक्ष आणि y-अक्षाच्या छेदनबिंदावर स्थित असलेल्या युनिट सर्कलने कोन मोजण्याच्या आधारे सायन, कोसाइन आणि टॅन्जेंट मूल्यांचे मूल्यांकन करण्यासाठी एक स्पष्ट संदर्भ फ्रेम प्रदान करते. जेव्हा कोन θ 0° वर सेट केला जातो, तेव्हा संबंधित त्रिकोणमितीय मूल्ये स्पष्ट असतात: 0° चा कोसाइन 1 असतो, सायन 0 असतो, आणि टॅन्जेंट, जो सायनच्या कोसाइनच्या प्रमाणात असतो, तो देखील 0 असतो. 

तुलनात्मकपणे, जेव्हा θ 90° होते, तेव्हा कोसाइन 0 वर जातो, तर सायन 1 वर पोहोचतो, ज्यामुळे टॅन्जेंट अनिर्धारित होतो, कारण शून्याने विभाजन होते. युनिट सर्कलचा खोलवर अभ्यास सायन, कोसाइन आणि टॅन्जेंटच्या सकारात्मक आणि नकारात्मक मूल्यांमधील परस्परसंवाद दर्शवतो, जो कार्टेशियन समन्वयांद्वारे नियंत्रित केला जातो. 

ही गतिशीलता विविध कोन मोजण्याची परवानगी देते, वापरकर्त्यांना युनिट सर्कलसह संवाद साधण्यास प्रोत्साहित करते जेणेकरून मूल्यांमध्ये होणाऱ्या या बदलांचे निरीक्षण करता येईल. 

युनिट सर्कलच्या हृदयात पायथागोरसचा प्रमेय आहे, जो सांगतो की एका उजव्या त्रिकोणात, हायपोटेनसचा वर्ग म्हणजे इतर दोन बाजांचा वर्गाची बेरीज. 

युनिट सर्कलसाठी, हा प्रमेय x² + y² = 1 या समीकरणात साधा होतो, जिथे x कोसाइनचे प्रतिनिधित्व करते आणि y सायनचे प्रतिनिधित्व करते. ही संबंधितता एक मूल्यवान त्रिकोणमितीय ओळख म्हणून संपन्न होते: (cos(θ))² + (sin(θ))² = 1. 

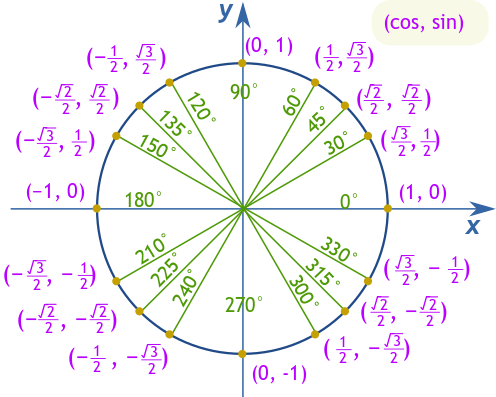
30°, 45°, आणि 60° सारख्या मुख्य कोनांवर नेव्हिगेट करण्यासाठी, त्यांच्या सायन, कोसाइन, आणि टॅन्जेंट मूल्यांचे स्मरण करणे फायदेशीर आहे. उदाहरणार्थ, 30° वर, कोसाइन √3/2 आहे, सायन 1/2 आहे, आणि टॅन्जेंट √3/3 आहे. 45° वर, सायन आणि कोसाइन दोन्ही √2/2 आहेत, ज्यामुळे टॅन्जेंट 1 मिळतो. अखेरीस, 60° वर, कोसाइन 1/2 आहे, सायन √3/2 आहे, आणि टॅन्जेंट √3 पर्यंत वाढतो. 

या मूल्यांना लक्षात ठेवण्यासाठी एक स्मरणशक्ती म्हणजे कोसाइनला कमी होत जाणाऱ्या संख्यांसोबत (3, 2, 1) आणि सायनला वाढत जाणाऱ्या संख्यांसोबत (1, 2, 3) संबंधित करणे. 

या तंत्राने शिकणे सोपे होते आणि स्मरणशक्ती वाढवते. टॅन्जेंट संदर्भात, जो सायनचा कोसाइनशी असलेला प्रमाण आहे, वापरकर्ते प्रत्येक कोनासाठी मूल्ये सहजपणे काढू शकतात. उदाहरणार्थ, tan(30°) सायन(30°)/कोसाइन(30°) म्हणून गणना केली जाते, ज्यामुळे √3/3 प्राप्त होते. तसाच, tan(45°) आणि tan(60°) च्या मूल्यांचा सहजतेने निकाल लावला जाऊ शकतो. 

स्मरणशक्ती वाढवण्यासाठी, या कोनांसाठी संबंधित त्रिकोणांची रेखाचित्रे काढणे फायदेशीर ठरू शकते. उदाहरणार्थ, 2 लांबीच्या बाजूंसह एक त्रिकोण काढणे आणि त्याचे विभाजन करणे, पायथागोरसच्या प्रमेयाचा उपयोग करून बाजूंची लांबी काढण्यात मदत करेल, जे अखेरीस सायन आणि कोसाइनच्या मूल्यांचे समजण्यास मदत करेल. 

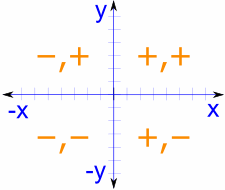
एक व्यापक साधन म्हणून, युनिट सर्कल सर्व चौकांना समाविष्ट करते, कोसाइन आणि सायन मूल्यांच्या चिन्हांचे समायोजन करते. या बारीक समजून घेणे पहिल्या चौकाच्या बाहेर मूल्यमापन करण्यासाठी महत्त्वाचे आहे. 

अखेर, युनिट सर्कल त्रिकोणमितीय कार्यांचे दृश्य प्रतिनिधित्व प्रदान करते, तर ते त्रिकोणमितीत एक मूलभूत संकल्पना म्हणून कार्य करते, जी विद्यार्थ्यांसाठी आणि व्यावसायिकांसाठी आवश्यक आहे. याची साधेपणा गणितीय तत्त्वांचा गहन समज वाढवण्यासाठी महत्त्वाचे आहे, त्यामुळे ते त्रिकोणमितीय अभ्यासाची एक आधारभूत गोष्ट बनते.