यूनिट सर्कल: त्रिकोणमिति में एक मौलिक उपकरण यूनिट सर्कल, जिसे एक की त्रिज्या वाले वृत्त के रूप में परिभाषित किया गया है, कोणों और लंबाई से संबंधित त्रिकोणमितीय अवधारणाओं को समझने के लिए एक आवश्यक उपकरण है। 

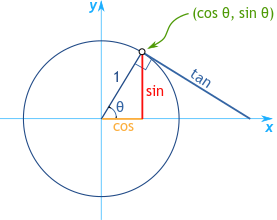ग्राफ पर x-अक्ष और y-अक्ष के चौराहे पर स्थित, यूनिट सर्कल कोण माप के आधार पर साइन, कोसाइन और टैंजेंट मानों का मूल्यांकन करने के लिए एक स्पष्ट संदर्भ प्रदान करता है। जब कोण, जिसे θ के रूप में दर्शाया गया है, 0° पर सेट होता है, तो संबंधित त्रिकोणमितीय मान सीधे होते हैं: 0° का कोसाइन 1 है, साइन 0 है, और टैंजेंट, जो साइन और कोसाइन का अनुपात है, वह भी 0 है। 

इसके विपरीत, जब θ 90° तक पहुँचता है, तो कोसाइन 0 पर गिर जाता है जबकि साइन 1 पर पहुँच जाता है, जिससे टैंजेंट अव्यवस्थित हो जाता है क्योंकि यह शून्य से विभाजित होता है। यूनिट सर्कल की गहरी पड़ताल साइन, कोसाइन और टैंजेंट के सकारात्मक और नकारात्मक मानों के बीच के अंतर्संबंध को प्रकट करती है, जो कार्टेशियन निर्देशांकों द्वारा निर्धारित होती है। 

यह गतिशीलता विभिन्न कोण मापों की अनुमति देती है, जिससे उपयोगकर्ता यूनिट सर्कल के साथ इंटरैक्टिव रूप से प्रयोग कर सकते हैं और इन मानों में बदलाव देख सकते हैं। 

यूनिट सर्कल के केंद्र में पाइथागोरस का प्रमेय है, जो यह утвержित करता है कि एक समकोण त्रिकोण में, कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है। 

यूनिट सर्कल के लिए, यह प्रमेय सरलता से समीकरण x² + y² = 1 में बदलता है, जहाँ x कोसाइन को दर्शाता है और y साइन को। यह संबंध एक मूल्यवान त्रिकोणमितीय पहचान में परिणत होता है: (cos(θ))² + (sin(θ))² = 1. 

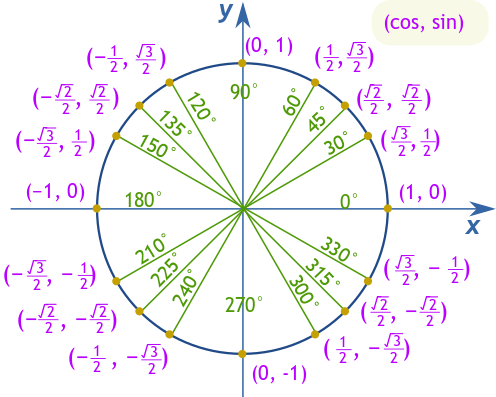
30°, 45°, और 60° जैसे प्रमुख कोणों को नेविगेट करने के लिए, उनके साइन, कोसाइन और टैंजेंट मानों को याद रखना फायदेमंद है। उदाहरण के लिए, 30° पर, कोसाइन √3/2 है, साइन 1/2 है, और टैंजेंट √3/3 है। 45° पर, साइन और कोसाइन दोनों √2/2 के बराबर होते हैं, जिससे टैंजेंट 1 प्राप्त होता है। अंत में, 60° पर, कोसाइन 1/2 है, साइन √3/2 है, और टैंजेंट √3 तक बढ़ जाता है। 

इन मानों को याद रखने में मदद करने के लिए एक स्मरण तकनीक में कोसाइन को घटते अंकों (3, 2, 1) और साइन को बढ़ते अंकों (1, 2, 3) के साथ जोड़ना शामिल है। 

यह तकनीक सीखने को सरल बनाती है और याददाश्त बनाए रखने में सहायता करती है। टैंजेंट के मामले में, जो साइन और कोसाइन के अनुपात के रूप में गणना की जाती है, उपयोगकर्ता प्रत्येक कोण के लिए मान आसानी से प्राप्त कर सकते हैं। उदाहरण के लिए, tan(30°) को sin(30°)/cos(30°) के रूप में गणना किया जाता है, जो √3/3 का परिणाम देता है। इसी तरह, tan(45°) और tan(60°) के लिए मान आसानी से निकाले जा सकते हैं। 

याददाश्त को मजबूत करने के लिए, इन कोणों के अनुरूप त्रिकोणों को खींचना फायदेमंद हो सकता है। उदाहरण के लिए, 2 की भुजाओं वाले त्रिकोण को खींचना और उसे विभाजित करना पाइथागोरस के प्रमेय को लागू करने में मदद करता है, जिससे भुजाओं की लंबाई ज्ञात करने में सहायता मिलती है, अंततः साइन और कोसाइन के मानों को समझने में सहायता मिलती है। 

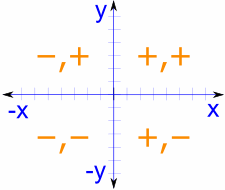
एक व्यापक उपकरण के रूप में, यूनिट सर्कल सभी चतुर्थांशों को समेटे हुए है, कोसाइन और साइन मानों के संकेतों को तदनुसार समायोजित करता है। यह सूक्ष्म समझ पहले चतुर्थांश के बाहर मानों को निर्धारित करने के लिए महत्वपूर्ण है। 

अंत में, यूनिट सर्कल केवल त्रिकोणमितीय कार्यों का दृश्य प्रतिनिधित्व प्रदान करने के लिए नहीं है, बल्कि यह त्रिकोणमिति में एक मौलिक अवधारणा के रूप में कार्य करता है, जो छात्रों और प्रैक्टिशनरों दोनों के लिए आवश्यक है। इसकी सरलता इसके महत्व को छुपाती है, जो गणितीय सिद्धांतों की गहरी समझ को सुविधाजनक बनाने में सहायक होती है, इसे त्रिकोणमितीय अध्ययन का एक आधार बनाती है।