ইউনিট চক্র: ত্ৰিকোণমিতিত এটা আধাৰিক সঁজুলি ইউনিট চক্র, যি এটা একক ৰেডিয়াছৰ চক্র হিচাপে পৰিচিত, কোণ আৰু দৈৰ্ঘ্যৰ সৈতে সম্পৰ্কিত ত্ৰিকোণমিতিৰ ধাৰণাসমূহ বুজিবলৈ এটা অত্যাৱশ্যকীয় সঁজুলি হিচাপে কাম কৰে। 

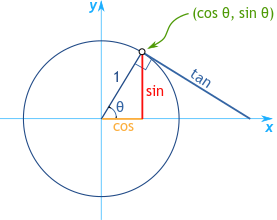গ্ৰাফত x-অক্ষ আৰু y-অক্ষৰ সংযোগস্থলে অৱস্থিত, ইউনিট চক্রে কোণৰ মাপৰ আধাৰত সিন, কোছাইন আৰু টেঞ্জেন্টৰ মান মূল্যায়ন কৰিবলৈ এটা স্পষ্ট উল্লেখ স্থান প্ৰদান কৰে। যেতিয়া কোণ, যাক θ হিচাপে চিহ্নিত কৰা হৈছে, 0° ত স্থাপন কৰা হয়, তেতিয়া সঙ্গত ত্ৰিকোণমিতি মানসমূহ সোজা: 0° ৰ কোছাইন 1, সিন 0, আৰু টেঞ্জেন্ট, যিটো সিনৰ আৰু কোছাইনৰ অনুপাত, 0 হৈছে। 

বিপৰীতে, যেতিয়া θ 90° ত পৌঁছায়, তেতিয়া কোছাইন 0লৈ হ্ৰাস পায় আৰু সিন 1 ত উচ্চতম অৱস্থালৈ যায়, টেঞ্জেন্ট শূন্যত বিভাজন হোৱাৰ বাবে অজ্ঞাত হৈ যায়। ইউনিট চক্রৰ গভীৰ অনুসন্ধানে সিন, কোছাইন, আৰু টেঞ্জেন্টৰ ধনাত্মক আৰু ঋণাত্মক মানসমূহৰ পৰস্পৰ সংযোগক প্ৰকাশ কৰে, যি কাৰ্টেছিয়ান সমন্বয়ৰ দ্বাৰা নিৰ্দেশিত। 

এই গতিশীলতাই কোণৰ মাপৰ এক বিস্তৃত বৈচিত্ৰ্যৰ অনুমতি দিয়ে, ব্যৱহাৰকাৰীবোৰক ইউনিট চক্রৰ সৈতে আন্তৰিকভাৱে পৰীক্ষা কৰিবলৈ অনুৰোধ কৰে যাতে এই মানসমূহৰ পৰিৱৰ্তনবোৰ লক্ষ্য কৰিব পাৰে। 

ইউনিট চক্রৰ কেন্দ্ৰত পিথাগৰাছৰ তত্ত্ব আছে, যি কথা কয় যে এটা সোঁতত, হাইপটেনিউজৰ বৰ্গ আন দুই পৃষ্ঠাৰ বৰ্গৰ যোগফলৰ সমান। 

ইউনিট চক্রৰ বাবে, এই তত্ত্বটো চাৰ্টে x² + y² = 1 ৰূপে সহজ হয়, য'ত x কোছাইনক আৰু y সিনক প্ৰতিনিধিত্ব কৰে। এই সম্পৰ্কটোৱে এটা মূল্যবান ত্ৰিকোণমিতি পৰিচয়ত পৰিণতি লাভ কৰে: (cos(θ))² + (sin(θ))² = 1. 

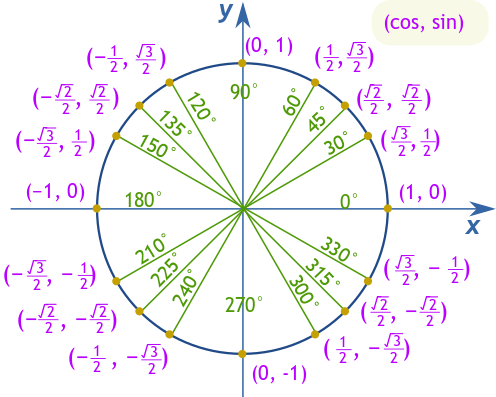
৩০°, ৪৫°, আৰু ৬০° যিমান পৰ্যায়ৰ কোণ গোৱাই, তেওঁলোকৰ সিন, কোছাইন, আৰু টেঞ্জেন্টৰ মানসমূহ স্মৰণ কৰা উপকাৰী। উদাহৰণস্বৰূপ, ৩০° ত কোছাইন √3/2, সিন 1/2, আৰু টেঞ্জেন্ট √3/3। ৪৫° ত, দুয়ো সিন আৰু কোছাইন √2/2 সমান, যাৰ ফলত টেঞ্জেন্ট 1। শেষত, ৬০° ত কোছাইন 1/2, সিন √3/2, আৰু টেঞ্জেন্ট √3 লৈ বৃদ্ধি পায়। 

এই মানবোৰ স্মৰণ কৰাত সহায় কৰিবলৈ এটা স্মৰণিকা অন্তর্ভুক্ত কৰে, য'ত কোছাইনক নিম্নমানৰ সংখ্যা (৩, ২, ১) আৰু সিনক উচ্চমানৰ সংখ্যা (১, ২, ৩) সৈতে সংযুক্ত কৰা হয়। 

এই প্ৰক্ৰিয়াই অধ্যয়নক সহজ কৰি তোলে আৰু স্মৃতিৰ ৰক্ষণাবেক্ষণ বৃদ্ধিত সহায় কৰে। টেঞ্জেন্টৰ ক্ষেত্ৰত, যিটো সিনৰ আৰু কোছাইনৰ অনুপাতে গণনা কৰা হয়, ব্যৱহাৰকাৰীসকলৰ বাবে প্ৰতিটো কোণৰ মান সহজেই উলিয়াব পৰা যায়। উদাহৰণস্বৰূপ, tan(৩০°) হৈছে sin(৩০°)/cos(৩০°), য'ত ফলাফল √3/3। তেনেদৰে, tan(৪৫°) আৰু tan(৬০°)ৰ মানবোৰ সহজে উলিয়াব পৰা যায়। 

স্মৃতিৰ দৃঢ়ীকৰণৰ বাবে, এই কোণবোৰৰ সৈতে সঁপা ত্ৰিভুজবোৰ আঁকিব পৰা উপকাৰী। উদাহৰণস্বৰূপ, ২ৰ দৈৰ্ঘ্যৰ এটা সঁপা ত্ৰিভুজ আঁকিলে আৰু বিভাজন কৰিলে, তেতিয়া পিথাগৰাছৰ তত্ত্বৰ প্ৰয়োগ কৰি পৃষ্ঠাৰ দৈৰ্ঘ্যসমূহ বিচাৰি পোৱাৰ পৰা সহায় হয়, যাৰ ফলত সিন আৰু কোছাইন মানবোৰৰ বুজাবুজিত সহায় হয়। 

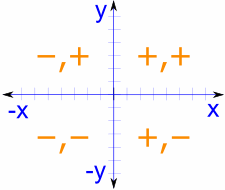
এটা বিস্তৃত সঁজুলি হিচাপে, ইউনিট চক্র সকলো চতুৰ্ভুজক অন্তর্ভুক্ত কৰে, কোছাইন আৰু সিনৰ মানসমূহৰ চিহ্নসমূহ যথাযথভাৱে সলনি কৰি। এই সূক্ষ্ম বুজাবুজি প্ৰথম চতুৰ্ভুজৰ বাহিৰে মানসমূহ নিৰ্ধাৰণ কৰাত অত্যন্ত গুৰুত্বপূর্ণ। 

উপসংহাৰত, ইউনিট চক্রে ত্ৰিকোণমিতি ফাংশনসমূহৰ চিত্ৰৰ প্ৰতিনিধিত্বৰ বাহিৰে, ত্ৰিকোণমিতিত এটা আধাৰিক ধাৰণা হিচাপে কাম কৰে, যি ছাত্ৰ আৰু ব্যৱসায়ীসকলৰ বাবে অত্যাৱশ্যক। ইয়াৰ সৰলতা ইয়াৰ গুৰুত্বৰ প্ৰতীক, যি গাণিতিক নীতিৰ গভীৰ বুজাবুজি প্ৰৱাহিত কৰাৰ ক্ষেত্ৰত সহায় কৰে, যিয়ে ইয়াক ত্ৰিকোণমিতি অধ্যয়নৰ এটা মূখ্য স্থান বানাইছে।